Arquivo do blog

quinta-feira, 24 de outubro de 2019

EQUAÇÃO DO 1º GRAU :Sugestões de Atividades


EQUAÇÃO DE 1º GRAU


Equação do 1º grau (primeiro grau) é nada mais do que uma igualdade entre as expressões, que as transformam em uma identidade numérica, para um ou para mais valores atribuídos as suas variáveis. A incógnita é o valor que precisamos achar para encontrar a solução para a equação. A variável que não conhecemos (incógnita) costumamos representá-la na equação pelas letras x, y e z.

Numa equação do primeiro grau, o expoente da incógnita é sempre 1.
Exemplo:
  • 5 + x = 8      Essa equação se transforma numa identidade, fazendo:
  • x = 3 ⇒ 5 + x = 8 ⇒   5 + 3 = 8  ⇒ 8 = 8  temos uma identidade.
A letra x na equação é denominada a variável da equação ou incógnita, enquanto que o número 3 é chamado de solução da equação, conjunto verdade ou raiz.
Na equação acima, o que está antes da igualdade é chamado de primeiro membro, e o que está do lado direito é chamado de segundo membro da equação.
Exemplo:
  • 3x – 12 (1º membro) = 7 + x(2º membro)

Tipos de equações

As equações podem ter uma ou mais incógnitas ou variáveis, como queira chamar:
Exemplos:
  • 4 + 2x = 11 + 3x (uma incógnita ou uma variável, a variável x)
  • y – 1 = 6x + 13 – 4y (duas incógnitas ou duas variáveis, x e y)
  • 8x – 3 + y = 4 + 5z – 2 (três incógnitas ou três variáveis, x,y e z)
Observação: não importa se a variável apareceu várias vezes, o que conta é quantas variáveis diferentes tem na equação.
Exemplo: x + 1 = x + 2, temos uma variável, o x, e não duas, não é a quantidade que levamos em conta.

Equações numéricas

É a equação que não tem nenhuma outra letra diferente a não ser a das incógnitas.
Exemplo:
  • x – 5 = -2x + 22

Equações literais

Toda equação que contém outra letra, além das que representam as variáveis.
Exemplo:
  • 3ax – 5 = ax + 4 (variável é x)

Como resolver uma equação de primeiro grau?

Para resolver uma equação do primeiro grau deve-se levar em consideração que ao mudarmos as variáveis (incógnitas) e os valores numéricos de posição na equação, a igualdade deve continuar sendo verdadeira.
Também devemos ficar atento com o sinal de cada variável ou valor numérico, pois para que a igualdade continue valendo devemos inverter o sinal ao mudar de lado na equação, apenas quando se trata de uma adição ou subtração.
Dessa forma, uma multiplicação passa para o outro lado dividindo, uma divisão passa multiplicando, uma subtração passa somando e uma soma passa subtraindo. Veja:
Exemplo: Encontrar o valor de x na equação: 3x + 2 = x + 1
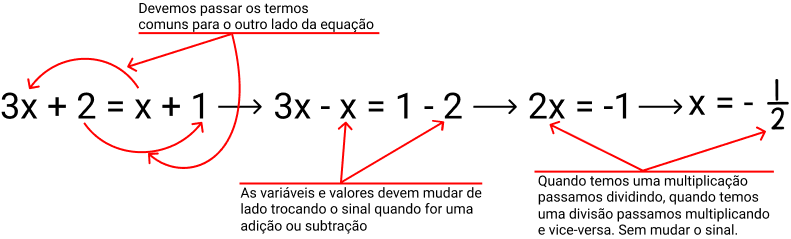
Como resolver uma equação do 1º grau (primeiro grau)
Dessa forma, o valor da variável x que torna a equação verdadeira é –1⁄2.
Vamos ver outro exemplo.
Exemplo: Encontrar o valor de x para a equação: -5x = -5
Existem duas formas de responder essa equação, multiplicando os dois lados por -1, para tornar toda a equação positiva ou manter o sinal e lembrar que durante a divisão de dois números negativos o sinal muda para positivo. Veja:

Equação do 1º grau solução

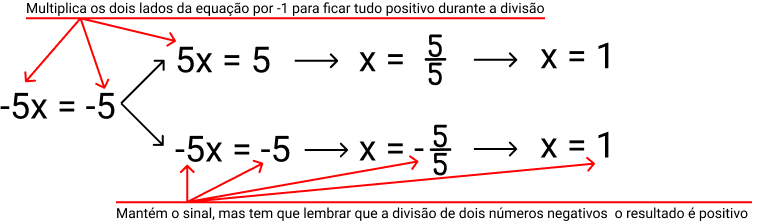
Como resolver uma equação do 1º grau (primeiro grau)


Atenção: sempre pode-se multiplicar os dois lados por -1, apesar de ser mais útil quando o lado que possui a incógnita for negativo.

Lista de exercícios com gabarito:


Sugestóes de atividades online:




Atividades para fixação no AEE

Vídeo para explicar a resolução da Equação do 1º grau


Atividade:

Dar as equações seguintes para o aluno resolver:

6x + 3 = 4x + 5 

10x – 9 = 21 + 2x + 3x 

10 – (8x – 2) = 5x + 2(– 4x + 1)  

x − 4 = 3 

4x − 9 = 23 

x + 5 = 8 

9x – 2 = 4x + 18 

3x = 15 

x − 1 = 5 

2(x + 5 ) – 4 = 26

Confome o aluno resolve, ele vai colocando o prendedor nos números referentes ao resultado da equação


AULA EXPOSITIVA E PROBLEMAS SOBRE EQUAÇÕES DO 1º GRAU

 Atividades: (Fonte: Dante 2016) Passe da linguagem usual para uma expressão algébrica:

a) Cinco menos um número: _______________________
b) O dobro de um número mais sete: _________________ 
c) Um número dividido por quatro: ___________________ 

(Fonte: Autora) Monte a equação referente a sentença a seguir: “Pensei em um número, adicionei 4, tirei 2 e obtive 10. Em que número pensei?

 TESTE INVESTIGATIVO

Colégio Estadual _________________________________________________. 
Nome: __________________________ nº _____ 7º _____ Data: ___/___/ ___. 

1) Para cada sentença, passe da linguagem usual para uma expressão algébrica: 
a) Pensei em um número e adicionei a 4 ________________________ 
b) O dobro de um número, subtraído 8 __________________________ 
c) Um número adicionado a um terço desse número _______________ 

 Sabendo-se que “x” é a variável, calcule o valor numérico em cada caso: 

a) 3x – 4, para x = 2 
b) 2x + 8, para x = -3 

 Resolva as seguintes situações:
a) Pensei em um número, adicionei a cinco e obtive 48. Que número pensei? 
b) Um número adicionado a seu triplo é igual a 16. Que número é esse? 
c) O dobro de um número subtraído 3 é igual a esse número adicionado a doze. Qual é esse número? 
d) Letícia pensou em um número, adicionou a sua metade e obteve 12. Que número Letícia pensou?

Resolva as equações: 
a) x + 15 = 35 
b)3x – 4 = 28 
c) 2( x – 2 ) = 16 
d) 3z – 10 = z + 60


JOGOS:

 DOMINÓ

TABULEIRO
Imagem disponível em: http://escolasec21.blogspot.com.br/2016/03/jogo-equacoes-do-1-grau.html. Acesso em 10/12/2016.

CRUZADINHA 

JOGO DOS QUADRADOS

É HORA DE JOGAR 

Público Alvo

A partir da 9ª série/9º ano.
Competências e Habilidades:
Obter o dominio no cálculo mental usando as quatro operações fundamentais com números naturais em equações de 1º grau, despertar interesse pelos ensinamentos matemáticos básicos, raciocínio e convívio social.
Material:
28 peças/pedras com diferentes inscrições de equações de primeiro grau, utilizando das quatro operações matemáticas básicas.
O Jogo
 Número de Participantes:
  • 2 - um contra o outro.
  • de 4 a 6 - em equipes de 2 ou 3 jogadores.
 Objetivo(s):
O jogador/equipe liberar todas as suas peças/pedras da mão.
 Regras:
  1. Os participantes devem jogar um contra o outro ou estar em um grupo de até 3 pessoas (totalizando 6 jogadores);
  2. Os jogadores devem sentar-se intercalados de acordo com os times, sempre colocando uma pessoa do grupo 1 e em seguida outra do grupo 2.
  3. Cada participante receberá um número de peças equivalente ao 'número total de peças dividido pelo número total de jogadores', mantendo a proporção jogadores/peças;
  4. A pedra de saída será a x = -1 e x = -1 (nomeada como a peça 0);
  5. O próximo a jogar será aquele que estiver à direita do iniciante do jogo;
  6. O jogador deve encaixar sua peça/pedra na mesa conforme as pedras presentes nas pontas do caminho formado pelo dominó, seguindo as regras do dominó tradicional, porém utilizando da resolução de equações de primeiro grau.
    6.1 O jogador que não conseguir encaixar nenhuma pedra/peça nem seu turno deverá ceder sua vez ao próximo adversário da fila.
  7. O vencedor será aquele, jogador ou time, que primeiro encaixar, no caminho/dominó exposto na mesa, todas as suas peças/pedras;
  8. Caso haja "fechamento" da partida, o vencedor, jogador ou time, será aquele que estiver com a menor quantidade de peças/pedras em mãos.
Fonte: elaborada pelos autor(es).

 2- Jogo das Equações 
Número de participantes: 3 ou 4 
Materiais: papel sulfite de cores diferentes 

Preparando o jogo:  Providenciar duas folhas de papel sulfite de cores diferentes;  Dividir cada folha em 12 partes iguais como mostram as figuras abaixo;  Em uma das folhas escrever as equações;  Na outra folha as soluções;  

Recortar 24 peças. 
Modo de Jogar: Em cada rodada os participantes misturam as peças e as repartem igualmente. No caso de 3 participantes, cada um fica com 4 fichas de cada cor. No caso de 4 participantes, cada um fica com 3 fichas de cada cor. Ao receber as fichas, cada jogador as verifica e marca um ponto toda vez que tiver uma ficha com a equação e a ficha com sua solução. Por exemplo:


O mesmo deve ser feito nas rodadas seguintes. Os pontos devem ser anotados em uma folha de sulfite à parte. Vence quem primeiro fizer 5 pontos.


Mais fontes:


Postado por às

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)